中3生必見!今回は中3で習う「有理数と無理数」の話。この記事を読めば、一瞬で無理数を判別できるようになります!
数の世界を広げよう

今回は中3数学「有理数と無理数」についての記事です。
第2章で「平方根(√)」の分野になります。
数学で扱う「数(かず)」には様々なものがあります。
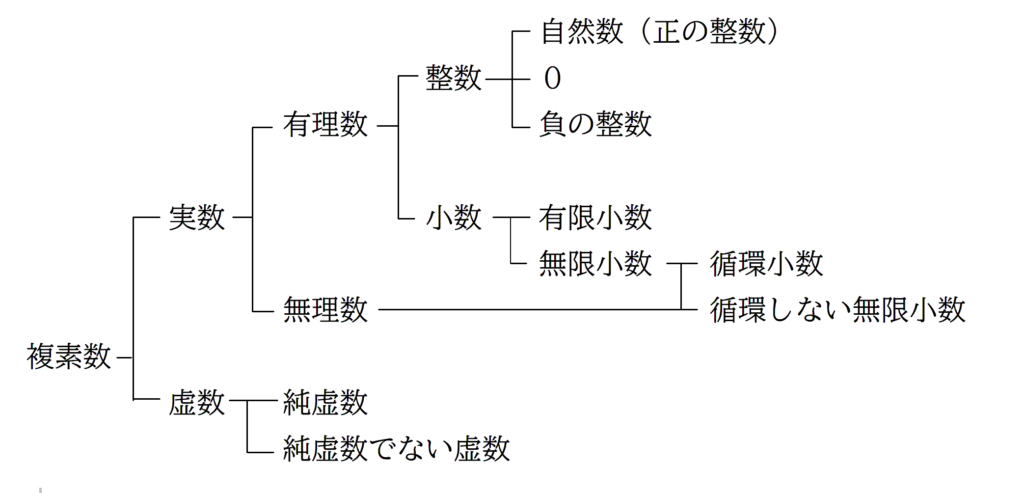
自然数、整数、分数、有限小数、循環小数、無限小数、
実数、有理数、無理数、虚数、複素数…などです。
中学履修範囲外もありますが、こうして書き出すと多いですね(笑)
では、1つ1つ解説していきます。
第2章で「平方根(√)」の分野になります。
数学で扱う「数(かず)」には様々なものがあります。
自然数、整数、分数、有限小数、循環小数、無限小数、
実数、有理数、無理数、虚数、複素数…などです。
中学履修範囲外もありますが、こうして書き出すと多いですね(笑)
では、1つ1つ解説していきます。
実数と虚数(複素数)
まずはじめに、「実数と虚数(複素数)」です。
これは高校で習いますが、中3の教科書などで発展の内容として
紹介してあることもあります。
ここで覚えていてほしいのが、
「中学校までの数は実数である」ということです。
複素数についてはこの記事では省きますが、簡単に説明すると
「2乗して−1 を満たす数」を 「i( 虚数単位)」といい、
実数 a, b を係数として表される数 a + bi を複素数と呼びます。
「2乗してー1?そんな数ないじゃん!」と思うかもしれませんが、
中学生はそれでOKです(笑)
高校でより数の世界が広がるので楽しみにしておきましょう!
これは高校で習いますが、中3の教科書などで発展の内容として
紹介してあることもあります。
ここで覚えていてほしいのが、
「中学校までの数は実数である」ということです。
複素数についてはこの記事では省きますが、簡単に説明すると
「2乗して−1 を満たす数」を 「i( 虚数単位)」といい、
実数 a, b を係数として表される数 a + bi を複素数と呼びます。
「2乗してー1?そんな数ないじゃん!」と思うかもしれませんが、
中学生はそれでOKです(笑)
高校でより数の世界が広がるので楽しみにしておきましょう!
有理数

中学生が習うのはここからです。
まず、「有理数」を理解しましょう。
「有理数」とは「分数で表せる数」のことです。
「分数で表せる数」がいくつあるかわかりますか?
では、解説していきます。
まず、「有理数」を理解しましょう。
「有理数」とは「分数で表せる数」のことです。
「分数で表せる数」がいくつあるかわかりますか?
では、解説していきます。
整数
整数は
「正の整数(自然数)、0、負の整数」
に分類できますが、整数は「分母が1の分数」とできますね。
(例:3=3/1)
よって、整数は有理数となります。
「正の整数(自然数)、0、負の整数」
に分類できますが、整数は「分母が1の分数」とできますね。
(例:3=3/1)
よって、整数は有理数となります。
有限小数
小数は
「有限小数と無限小数」
に分類できます。
「ある位で終わる小数」を「有限小数」といいますが、
分母を10、100、1000・・・とすれば分数で表せますね。
(例:0.7=7/10 0.123=123/1000)
よって、有限小数は有理数です。
「有限小数と無限小数」
に分類できます。
「ある位で終わる小数」を「有限小数」といいますが、
分母を10、100、1000・・・とすれば分数で表せますね。
(例:0.7=7/10 0.123=123/1000)
よって、有限小数は有理数です。
無限小数
「無限に続く小数」を「無限小数」といいます。
わかりやすいですね(笑)
無限小数は
「循環小数と循環しない無限小数」
に分類できます。
「循環小数」とは、ある特定の数字の並び(循環節)が
繰り返し表れる無限小数のことです。
例えば、0.3333・・・、0.345345345・・・などです。
結論からいうと、循環小数は「有理数」となります。
0.3333・・・=1/3 0.345345345・・・=115/333
このように分数で表すことが出来るからです。
わかりやすいですね(笑)
無限小数は
「循環小数と循環しない無限小数」
に分類できます。
「循環小数」とは、ある特定の数字の並び(循環節)が
繰り返し表れる無限小数のことです。
例えば、0.3333・・・、0.345345345・・・などです。
結論からいうと、循環小数は「有理数」となります。
0.3333・・・=1/3 0.345345345・・・=115/333
このように分数で表すことが出来るからです。
無理数

無理数とは「分数で表せない数」のことです。
「分数にならない」と聞いてどんな数が思い浮かびましたか?
大事なことは、「無理数は中学生では2種類のみ!」ですので
しっかり覚えておきましょう。
「分数にならない」と聞いてどんな数が思い浮かびましたか?
大事なことは、「無理数は中学生では2種類のみ!」ですので
しっかり覚えておきましょう。
平方根(√)
まず1つ目は「平方根(√)」です。
平方根とは「2乗してもとの数になる数」です。
正と負の2つあるのを忘れずにしましょう。
例えば、25の平方根は5とー5、 7の平方根は√7とー√7
このうち、整数でない平方根は分数では表せません。
√2=1.41421356・・・のように無限小数となります。
また、特定の数字の並びが繰り返し表れてもいませんので、
循環小数でもありません。
つまり、無理数とは
「循環しない無限小数」といえますね!
平方根以外の「循環しない無限小数」がほかにもあります。
中学生のみなさん、思いつきますか?
ヒントは「文字で表せる数字」です。
平方根とは「2乗してもとの数になる数」です。
正と負の2つあるのを忘れずにしましょう。
例えば、25の平方根は5とー5、 7の平方根は√7とー√7
このうち、整数でない平方根は分数では表せません。
√2=1.41421356・・・のように無限小数となります。
また、特定の数字の並びが繰り返し表れてもいませんので、
循環小数でもありません。
つまり、無理数とは
「循環しない無限小数」といえますね!
平方根以外の「循環しない無限小数」がほかにもあります。
中学生のみなさん、思いつきますか?
ヒントは「文字で表せる数字」です。
π(円周率)
答えは「π(円周率)」です。
小学生までは、円周率=約3.14
として計算してきましたが、
中1でこの円周率をギリシャ文字の「π」で表すと習いましたね。
π=3.1415926535・・・
このように、「π」は「循環しない無限小数」
つまり、「無理数」になります。
高校では、このほかに「ネイピア数 e 」という数を習いますが、
この「e」も無理数です。
高校で勉強するのが楽しみですね!
小学生までは、円周率=約3.14
として計算してきましたが、
中1でこの円周率をギリシャ文字の「π」で表すと習いましたね。
π=3.1415926535・・・
このように、「π」は「循環しない無限小数」
つまり、「無理数」になります。
高校では、このほかに「ネイピア数 e 」という数を習いますが、
この「e」も無理数です。
高校で勉強するのが楽しみですね!
まとめ

最後にまとめておきましょう。
「無理数」とは、
「分数で表せない数」であり、「循環しない無限小数」です。
つまり、中学生の無理数は、「整数にならない√」と「π」の2つ!!
この2つ以外は、すべて「有理数」です。
これですぐに「有理数と無理数」を分類できますね!
定期テストでよく「無理数を選べ」と出題されるので
覚えておきましょう。
中学生の皆さん、数学は楽しい学問です。
勉強頑張ってください!
「無理数」とは、
「分数で表せない数」であり、「循環しない無限小数」です。
つまり、中学生の無理数は、「整数にならない√」と「π」の2つ!!
この2つ以外は、すべて「有理数」です。
これですぐに「有理数と無理数」を分類できますね!
定期テストでよく「無理数を選べ」と出題されるので
覚えておきましょう。
中学生の皆さん、数学は楽しい学問です。
勉強頑張ってください!
鹿児島県霧島市で学習塾をお探しの方へ
最後になりますが、この記事を書いているのは
鹿児島県霧島市にある「北辰塾」の塾長です。
現在も私立中・高で現役の数学教師として教壇に立っています。
北辰塾では単なる暗記ではなく、しっかりと「なぜそうなるのか?」ということを
意識して指導を行っています。
興味のある生徒、親御さんは一度、当塾へご連絡してください。
みなさんと一緒に勉強できるのを楽しみにお待ちしています。
鹿児島県霧島市にある「北辰塾」の塾長です。
現在も私立中・高で現役の数学教師として教壇に立っています。
北辰塾では単なる暗記ではなく、しっかりと「なぜそうなるのか?」ということを
意識して指導を行っています。
興味のある生徒、親御さんは一度、当塾へご連絡してください。
みなさんと一緒に勉強できるのを楽しみにお待ちしています。
